Було питання на твітері щодо того, як обчислити дотичний/tangent та бідотичний/bitangent вектори, знаючи тільки положення, \(UV\), та нормалю кожної вершини трикутника. У цьому пості я виведу формулу для вирішення цього задання. Ці вектори часто використовуються для відображення нормалей/normal mapping.
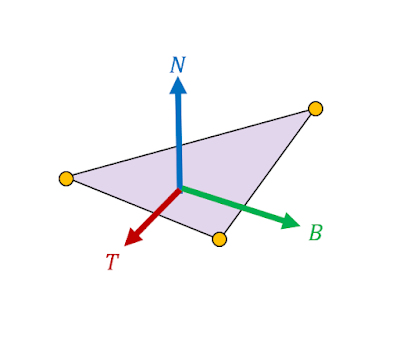
По-перше, що таке дотичний/бідотичний вектори? Це вектори, які разом із нормаллю утворюють систему координат. Нормаль вектор виходить від поверхні об'єкта, а дотичний/бідотичний вектори рухаються по поверхні об'єкта.
Дотичний/бідотичний вектори можуть бути будь-які вектори, які перпендикулярні та направлені вздовж поверхні об'єкта. Проте в графіці ми вже зберігаємо \(UV\) координати для кожної вершини, а \(UV\) координати утворюють двовимірну систему координат, яка орієнтована вздовж поверхні об'єкта. Тому ми зазвичай визначаємо дотичний вектор так, щоб його напрямок був таким самим як \(U\), а бідотичний вектор як \(V\).
Отже трикутник фактично існує у двох просторах одночасно: у просторі світу (коли використовуємо положення кожної вершини), та у дотичному просторі (коли використовуємо \(UV\) координати кожної вершини, це той самий простір, що і \(UV\) space):
Ми знаємо, що напрямки векторів \(U\) та \(V\) такі самі, як напрямки дотичного/бідотичного векторів, але ми хочемо знайти ці напрямки у просторі світу (у дотичному просторі, вони просто дорівнюють \(U = (1, 0), V = (0, 1)\)). Наприклад, положення вершини у просторі світу є перетвореним положенням вершини у просторі \(UV\) (і це саме хочемо знайти для цих двох векторів). Тому зараз, виведемо формулу яка обчислить вектор \(U\) та \(V\), у дотичному просторі, і перетворимо цю формулу щоб результат був у просторі світу.
Дані змінні:
\(UV_{0}, UV_{1}, UV_{2} \) - це положення кожної вершини у дотичному просторі
\(P_{0}, P_{1}, P_{2}\) - це положення кожної вершини у світовому просторі
\(T\) - це дотичний вектор у дотичному просторі
\(B\) - це бідотичний вектор у бідотичному просторі
Те, що шукаємо:
\(T'\) - це дотичний вектор у світовому просторі
\(B'\) - це бідотичний вектор у світовому просторі
Відтепер, якщо змінна має апостроф (наприклад \(T'\)), то це означає, що ця змінна знаходиться у світовому просторі. А якщо апострофа немає, то змінна у дотичному просторі. Тепер давайте зосередимося на трикутника у дотичному просторі:
Якщо обчислимо дельту UV координат між вершинами \(UV_0\) та \(UV_1\), то отримаємо \(\triangle U_1\) та \(\triangle V_1\). Ми бачимо, що \(triangle U_1\) має цей сам напрямок як \(T\), а \(\triangle V_1\) має той сам напрямок, що й \(B\). Можемо це формалізувати у цьому рівнянні:
\[ E_1 = UV_1 - UV_0 = \triangle U_1 \cdot T + \triangle V_1 \cdot B \]
де \(\triangle U_1\) і \(\triangle V_1\) це скаляри.
Уявімо, що ми не знаємо до чого \(T\) та \(B\) дорівнюють у цьому просторі. Тоді, у нас рівняння з двома невідомими змінними, тому нам потрібно отримати ще одне рівняння, щоб обчислити ці дві змінні. Ми можемо обчислити нове рівняння застосовуючи цей самий метод, що і попередньо, але тепер між \(UV_2\) та \(UV_1\):
\[ E_2 = UV_2 - UV_1 = \triangle U_2 \cdot T + \triangle V_2 \cdot B \]
Тепер у нас два рівняння та дві змінні, які ми хочемо обчислити:
\[ E_1 = \triangle U_1 \cdot T + \triangle V_1 \cdot B \]
\[ E_2 = \triangle U_2 \cdot T + \triangle V_2 \cdot B \]
Є багато способів вирішити цих двох змінних (метод підстановки, метод усунення), але я виведу формули для цих змінних застосовючи метод матриць. Спочатку перемінимо обидва верхні рівняння в одне матричне рівняння:
\begin{align*} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \\ \end{bmatrix} = \begin{bmatrix} \triangle U_1 & \triangle V_1 \\ \triangle U_2 & \triangle V_2 \\ \end{bmatrix} \begin{bmatrix} T_{x} & T_{y} & T_{z} \\ B_{x} & B_{y} & B_{z} \\ \end{bmatrix} \end{align*}
Ми хочемо отримати формулу, де права матриця залишається самою з одного боку рівняння, а всі інші матриці знаходяться з другого боку. Щоб так змінити цю формулу, обчислимо обернену матрицю наших дельт, і помножимо обидва боки рівняння на неї:
\begin{align*} \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1}\begin{bmatrix} \triangle V_2 & -\triangle V_1 \\ -\triangle U_2 & \triangle U_1 \\ \end{bmatrix} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \\ \end{bmatrix} = \begin{bmatrix} T_{x} & T_{y} & T_{z} \\ B_{x} & B_{y} & B_{z} \\ \end{bmatrix} \end{align*}
\begin{align*} \Rightarrow \begin{bmatrix} T_{x} & T_{y} & T_{z} \\ B_{x} & B_{y} & B_{z} \\ \end{bmatrix} = \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1}\begin{bmatrix} \triangle V_2 & -\triangle V_1 \\ -\triangle U_2 & \triangle U_1 \\ \end{bmatrix} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \\ \end{bmatrix} \end{align*}
І ось так, ми можемо обчислити дотичний/бідотичний вектори! Але ця формула обчислюється у дотичному просторі, а ми хочемо обчислити ці вектори у світовому просторі. Якщо ми перетворимо обидва боки цього рівняння до простору світу, то побачимо, що нам слід перемінити всі вектори до світового простору (отже \(E_1\), \(E_2\) перетворюються до \(E'_1\), \(E'_2\), а всі скаляри залишаються такими самими). Таким чином, ми отримаємо нашу кінцеву формулу. Якщо вас цікавить, як перетворити обидва боки цього рівняння до простору світу, то решта того посту покаже вам, як це зробити, та як вивести остаточні формули. А якщо ні, кінцева формула знаходиться на кінець цієї сторінки.
Ми знаємо що перетворення між дотичним простором та світовим простором є лінійним перетворенням (множення на матрицю). А лінійне перетворення задовольняє ці аксіоми:
\begin{align*} &\text{(1) Адитивність:} \quad L(\mathbf{u} + \mathbf{v}) = L(\mathbf{u}) + L(\mathbf{v}) \\ &\text{(2) Гомогенність:} \quad L(k\mathbf{u}) = kL(\mathbf{u}) \quad \text{для всіх скалярів } k \\ \end{align*}
де \(L\) це лінійне перетворення, а \(\mathbf{u}\), \(\mathbf{v}\) це вектори.
Таким чином, скажімо що функція \(L\) це лінійне перетворення від дотичного простору до простору світу. Використовимо її для перетворення наших рівнянь до простору світу. Тільки зауважте, у нас є матриці, а наші аксіоми визначаються тільки для скалярів або векторів. Тому спочатку я розмножу матриці з правого боку рівняння, а після напишу векторну форму нашого рівняння для \(T\) та \(B\):
\begin{align*} \begin{bmatrix} \triangle V_2 & -\triangle V_1 \\ -\triangle U_2 & \triangle U_1 \\ \end{bmatrix} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \\ \end{bmatrix}\end{align*}
\begin{align*} = \begin{bmatrix} (\triangle V_2 \cdot E_{1x} - \triangle V_1 \cdot E_{2x}) & (\triangle V_2 \cdot E_{1y} - \triangle V_1 \cdot E_{2y}) & (\triangle V_2 \cdot E_{1z} - \triangle V_1 \cdot E_{2z}) \\ (-\triangle U_2 \cdot E_{1x} + \triangle U_1 \cdot E_{2x}) & (-\triangle U_2 \cdot E_{1y} + \triangle U_1 \cdot E_{2y}) & (-\triangle U_2 \cdot E_{1z} + \triangle U_1 \cdot E_{2z}) \\ \end{bmatrix} \end{align*}
Тепер, перемінемо наше матричне рівняння до векторні форми:
\begin{align*} \begin{bmatrix} T_{x} \\ T_{y} \\ T_{z} \\ \end{bmatrix} = \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \begin{bmatrix} (\triangle V_2 \cdot E_{1x} - \triangle V_1 \cdot E_{2x}) \\ (\triangle V_2 \cdot E_{1y} - \triangle V_1 \cdot E_{2y}) \\ (\triangle V_2 \cdot E_{1z} - \triangle V_1 \cdot E_{2z}) \\ \end{bmatrix} \end{align*}
\begin{align*} \begin{bmatrix} B_{x} \\ B_{y} \\ B_{z} \\ \end{bmatrix} = \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \begin{bmatrix} (-\triangle U_2 \cdot E_{1x} + \triangle U_1 \cdot E_{2x}) \\ (-\triangle U_2 \cdot E_{1y} + \triangle U_1 \cdot E_{2y}) \\ (-\triangle U_2 \cdot E_{1z} + \triangle U_1 \cdot E_{2z}) \\ \end{bmatrix} \end{align*}
Я змінив вектори на стовпчиковi вектори, щоб все помістити у блог-пост :P. Ці дві формули разом створюють матричну формулу, але у такій формі можна застосовувати аксіоми лінійного перетворення. Почнемо перетворювати рівняння для \(T\) до простору світу:
\begin{align*} \Rightarrow L\left(\begin{bmatrix} T_{x} \\ T_{y} \\ T_{z} \\ \end{bmatrix}\right) = L\left(\frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \begin{bmatrix} (\triangle V_2 \cdot E_{1x} - \triangle V_1 \cdot E_{2x}) \\ (\triangle V_2 \cdot E_{1y} - \triangle V_1 \cdot E_{2y}) \\ (\triangle V_2 \cdot E_{1z} - \triangle V_1 \cdot E_{2z}) \\ \end{bmatrix}\right) \end{align*}
\begin{align*} \Rightarrow \begin{bmatrix} T'_{x} \\ T'_{y} \\ T'_{z} \\ \end{bmatrix} = L\left(\frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \cdot \left(\triangle V_2 \cdot \begin{bmatrix} E_{1x} \\ E_{1y} \\ E_{1z} \\ \end{bmatrix} - \triangle V_1 \cdot \begin{bmatrix} E_{2x} \\ E_{2y} \\ E_{2z} \\ \end{bmatrix}\right)\right) \end{align*}
через те, що \(T'\) - це \(T\) але у просторі світу.
\begin{align*} \Rightarrow \begin{bmatrix} T'_{x} \\ T'_{y} \\ T'_{z} \\ \end{bmatrix} = \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \cdot L\left(\triangle V_2 \cdot \begin{bmatrix} E_{1x} \\ E_{1y} \\ E_{1z} \\ \end{bmatrix} - \triangle V_1 \cdot \begin{bmatrix} E_{2x} \\ E_{2y} \\ E_{2z} \\ \end{bmatrix}\right) \end{align*}
застосовуючи гомогенність (2) (перший термін це скаляр).
\begin{align*} \Rightarrow \begin{bmatrix} T'_{x} \\ T'_{y} \\ T'_{z} \\ \end{bmatrix} = \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \cdot \left(L\left(\triangle V_2 \cdot \begin{bmatrix} E_{1x} \\ E_{1y} \\ E_{1z} \\ \end{bmatrix}\right) - L\left(\triangle V_1 \cdot \begin{bmatrix} E_{2x} \\ E_{2y} \\ E_{2z} \\ \end{bmatrix}\right)\right) \end{align*}
застосовуючи адитивність (1).
\begin{align*} \Rightarrow \begin{bmatrix} T'_{x} \\ T'_{y} \\ T'_{z} \\ \end{bmatrix} = \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \cdot \left(\triangle V_2 \cdot L\left(\begin{bmatrix} E_{1x} \\ E_{1y} \\ E_{1z} \\ \end{bmatrix}\right) - \triangle V_1 \cdot L\left(\begin{bmatrix} E_{2x} \\ E_{2y} \\ E_{2z} \\ \end{bmatrix}\right)\right) \end{align*}
застосовуючи гомогенність (2) (\(\triangle V_1\) та \(\triangle V_2\) - це скаляри).
Тепер, як ми можемо обчислити перетворення змінних \(E_1\) та \(E_2\)? Ну, ми маємо формули для цих змінних, які просто віднімають точки у дотичному просторі, отже ми також момежо відобразити їх з перетворенням \(L\):
\[ L\left(E_1\right) = L\left(UV_{1} - UV_{0}\right)\]
\[ \Rightarrow E'_1 = L\left(UV_{1}\right) - L\left(UV_{0}\right)\]
застосовуючи адитивність (2)
\[ \Rightarrow E'_1 = P_{1} - P_{0}\]
тому що \(P_0\) та \(P_1\) - це ті самі точки, але у просторі світу, до якого \(L\) відображає. Подібну формулу можемо отримати для \(E_2\):
\[ E'_2 = P_{2} - P_{1}\]
Це перетворює нашу формулу для \(Т'\) у наступне:
\begin{align*} \Rightarrow \begin{bmatrix} T'_{x} \\ T'_{y} \\ T'_{z} \\ \end{bmatrix} = \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \cdot \left(\triangle V_2 \cdot \begin{bmatrix} E'_{1x} \\ E'_{1y} \\ E'_{1z} \\ \end{bmatrix} + \triangle V_1 \cdot \begin{bmatrix} E'_{2x} \\ E'_{2y} \\ E'_{2z} \\ \end{bmatrix}\right) \end{align*}
І, як бачите, з правої сторони рівняння, ми використовуємо положення вершин у просторі світу (щоб обчислити \(E'_1\), \(E'_2\)) та \(UV\) координати, щоб обчислити змінні дельти, які є величинами, які нам відомі! І ця формула обчислює дотичний вектор у просторі світу, що є саме тим, що ми шукаємо! Подібну формулу можемо отримати для бідотичного вектора. Отже, ось остаточні формули:
\begin{align*} \begin{bmatrix} T'_{x} \\ T'_{y} \\ T'_{z} \\ \end{bmatrix} = \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \cdot \left(\triangle V_2 \cdot \begin{bmatrix} E'_{1x} \\ E'_{1y} \\ E'_{1z} \\ \end{bmatrix} - \triangle V_1 \cdot \begin{bmatrix} E'_{2x} \\ E'_{2y} \\ E'_{2z} \\ \end{bmatrix}\right) \end{align*}
\begin{align*} \begin{bmatrix} B'_{x} \\ B'_{y} \\ B'_{z} \\ \end{bmatrix} = \frac{1}{\triangle U_1 \triangle V_2 - \triangle U_2 \triangle V_1} \cdot \left(-\triangle U_2 \cdot \begin{bmatrix} E'_{1x} \\ E'_{1y} \\ E'_{1z} \\ \end{bmatrix} + \triangle U_1 \cdot \begin{bmatrix} E'_{2x} \\ E'_{2y} \\ E'_{2z} \\ \end{bmatrix}\right) \end{align*}
де
\[ E'_1 = P_{1} - P_{0}\] \[ E'_2 = P_{2} - P_{1}\] \[ \triangle U_1 = UV_{1x} - UV_{0x}\] \[ \triangle V_1 = UV_{1y} - UV_{0y}\] \[ \triangle U_2 = UV_{2x} - UV_{1x}\] \[ \triangle V_2 = UV_{2y} - UV_{1y}\]
І ось так, ми вивели формули, які обчислюють дотичний та бідотичний вектори, використовуючи дані у вершинах трикутника :)